LFSR Properties¶
- LFSR Properties: Test 3+1 properties of LFSR
Using test_properties(verbose=1) method, it we can test if LSFR set be state and polynomial setisfies the following properites in addition to periodicity (period T = 2^M -1) for M-bit LFSR
Balance Property
Runlength Property
Autocorrelation Property
Balance Property¶
In a period of LFSR with a valid feedback polynomial, the number of 1s should be equal to number of 0s +1
‘’ N1s == N0s + 1 ‘’
Test balance property for a given full period of seq, p.
import numpy as np
from pylfsr import LFSR
state = [1,1,1,1,0]
fpoly = [5,3]
L = LFSR(initstate=state,fpoly=fpoly)
p = L.getFullPeriod()
# Returns (Bool, (number of ones, number of zeros))
# bool is True, balance test is passed
L.balance_property(p.copy())
(True, (16, 15))
Runlength Property¶
Run Length Property: In a period of LSFR with valid feedback polynomial, the number of runs of different length are in specific order.
‘’ number of (M-k) bit runs = ⌈ 2^(k-1) ⌉ , for k = 0 to M-1 ‘’
where ⌈ ⌉ is a ceiling function That is, for M bit LFSR,
number of M bit runs : 1
number of (M-1) bit runs : 1
number of (M-2) bit runs : 2
number of (M-3) bit runs : 4
… so on
state = [1,1,1,1,0]
fpoly = [5,3]
L = LFSR(initstate=state,fpoly=fpoly)
p = L.getFullPeriod()
L.runlength_property(p.copy())
(True, array([8, 4, 2, 1, 1]))
Autocorrelation Property¶
Autocorrelation Property: For sequence of period T of LSFR with valid feedback polynomial, the autocorrelation is a noise like, that is, 1 with zero (or T) lag (shift), -1/T (almost zero) else. unlike usual, for binary, the correlation value between two sequence of same length bx, by is computed as follow; match = sum(bx == by) (number of mataches) mismatch = sum(bx!= by) (number of mismatches)
state = [1,1,1,1,0]
fpoly = [5,3]
L = LFSR(initstate=state,fpoly=fpoly)
p = L.getFullPeriod()
L.autocorr_property(p.copy())
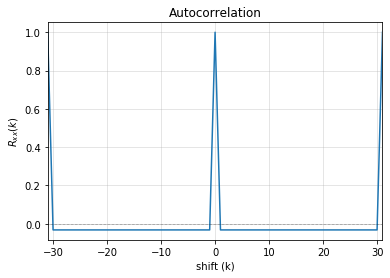
Test LFSR: p(x) = x5+ x2+1¶
Let’s test LFSR [5,3], for 5-bit LFSR, which we know is a primitive polynomial
state = [1,1,1,1,0]
fpoly = [5,3]
L = LFSR(initstate=state,fpoly=fpoly)
result = L.test_properties(verbose=2)
1. Periodicity
------------------
- Expected period = 2^M-1 = 31
- Pass?: True
2. Balance Property
-------------------
- Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) = (16, 15)
- Pass?: True
3. Runlength Property
-------------------
- Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
- Runs: [8 4 2 1 1]
- Pass?: True
4. Autocorrelation Property
-------------------
- Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
- Pass?: True
==================
Passed all the tests
==================
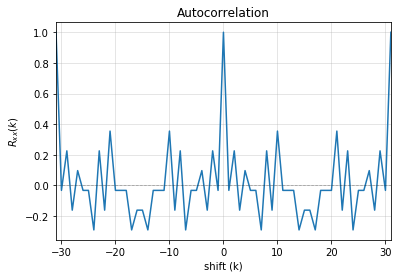
Test LFSR: p(x) = x5+ x1+1¶
Test LFSR [5,1], for 5-bit LFSR, which we know is *NOT* a primitive polynomial
state = [1,1,1,1,0]
fpoly = [5,1]
L = LFSR(initstate=state,fpoly=fpoly)
result = L.test_properties(verbose=2)
1. Periodicity
------------------
- Expected period = 2^M-1 = 31
- Pass?: False
2. Balance Property
-------------------
- Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) = (17, 14)
- Pass?: False
3. Runlength Property
-------------------
- Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
- Runs: [10 2 1 1 2]
- Pass?: False
4. Autocorrelation Property
-------------------
- Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
- Pass?: False
==================
Failed one or more tests, check if feedback polynomial is primitive polynomial
==================
Individual properties¶
state = [1,1,1,1,1]
fpoly = [5,4,3,2]
L = LFSR(initstate=state,fpoly=fpoly)
# get one full period
p = L.getFullPeriod()
L.balance_property(p.copy())
L.runlength_property(p.copy())
L.autocorr_property(p.copy())

